Prim's algoritme

In deze tutorial leer je hoe het algoritme van Prim werkt. Ook vindt u werkende voorbeelden van het algoritme van Prim in C, C ++, Java en Python.

Prim's algoritme is een minimum spanning tree-algoritme dat een grafiek als invoer neemt en de subset van de randen van die grafiek vindt die

vormen een boom die elk hoekpunt omvat
heeft de minimale som van gewichten tussen alle bomen die uit de grafiek kunnen worden gevormd

Hoe het algoritme van Prim werkt

Het valt onder een klasse van algoritmen die hebzuchtige algoritmen worden genoemd, die het lokale optimum vinden in de hoop een globaal optimum te vinden.

We beginnen bij één hoekpunt en blijven randen toevoegen met het laagste gewicht totdat we ons doel bereiken.

De stappen voor het implementeren van het algoritme van Prim zijn als volgt:

Initialiseer de minimum spanning tree met een willekeurig gekozen hoekpunt.
Zoek alle randen die de boom met nieuwe hoekpunten verbinden, zoek het minimum en voeg het toe aan de boom
Blijf stap 2 herhalen totdat we een minimale spanning tree hebben

Voorbeeld van het algoritme van Prim

Begin met een gewogen grafiek

Kies een hoekpunt

Kies de kortste rand van dit hoekpunt en voeg deze toe

Kies het dichtstbijzijnde hoekpunt dat nog niet in de oplossing staat

Kies de dichtstbijzijnde rand die nog niet in de oplossing staat, als er meerdere keuzes zijn, kies er dan een willekeurig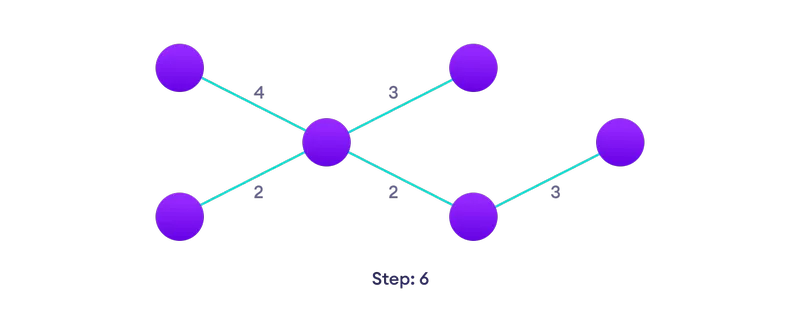

Herhaal tot je hebben een opspannende boom

Prim's algoritme pseudocode

De pseudocode voor het algoritme van prim laat zien hoe we twee sets hoekpunten U en VU maken. U bevat de lijst met vertices die zijn bezocht en VU de lijst met vertices die niet zijn bezocht. Een voor een verplaatsen we hoekpunten van set VU naar set U door de kleinste gewichtsrand te verbinden.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Python, Java en C / C ++ voorbeelden

Hoewel een aangrenzende matrixweergave van grafieken wordt gebruikt, kan dit algoritme ook worden geïmplementeerd met behulp van Adjacency List om de efficiëntie te verbeteren.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Prim's vs Kruskal's algoritme

Het algoritme van Kruskal is een ander populair algoritme voor minimum spanning tree dat een andere logica gebruikt om de MST van een grafiek te vinden. In plaats van te beginnen met een hoekpunt, sorteert het algoritme van Kruskal alle randen van laag naar hoog en voegt steeds de laagste randen toe, waarbij de randen die een cyclus creëren worden genegeerd.